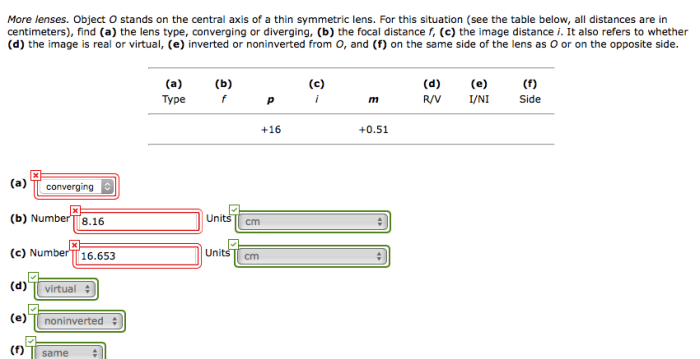
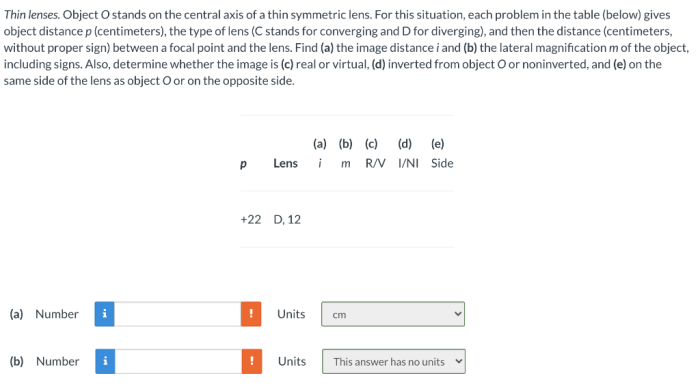
Thin lenses. object o stands on the central axis – In the realm of optics, thin lenses hold a pivotal role, manipulating light to form images that captivate our perception. This discourse delves into the intricate behavior of thin lenses when an object is positioned precisely on their central axis, unraveling the fundamental principles that govern image formation and its characteristics.
Thin lenses, characterized by their negligible thickness compared to their focal length, possess unique properties that enable them to converge or diverge light rays, creating real or virtual images. When an object is placed on the central axis of a thin lens, its image formation follows a set of well-defined rules, governed by the lens equation and the principles of ray tracing.
Basic Concepts

Thin lenses are optical devices that have a thickness that is much smaller than their radii of curvature. They are used in a wide variety of applications, including cameras, telescopes, and microscopes.
The key characteristics of thin lenses are their focal length and object distance. The focal length is the distance between the lens and the point where parallel rays of light converge after passing through the lens. The object distance is the distance between the lens and the object being imaged.
Object on Central Axis
When an object is placed on the central axis of a thin lens, the image is also formed on the central axis. The relationship between the object distance (d o), the image distance (d i), and the focal length (f) is given by the thin lens equation:
/f = 1/do+ 1/d i
Ray Tracing
Ray tracing is a technique that can be used to determine the image formed by a thin lens. To perform ray tracing, the following steps are followed:
- Draw a ray from the object to the center of the lens.
- Draw a ray from the object to the edge of the lens.
- The intersection of the two rays after they pass through the lens is the location of the image.
Lens Equation
The lens equation is a mathematical equation that relates the object distance, image distance, and focal length of a thin lens. The lens equation can be derived using the principles of geometric optics.
The lens equation is a powerful tool that can be used to calculate the image distance and magnification of a thin lens.
Image Characteristics, Thin lenses. object o stands on the central axis
The image formed by a thin lens has a number of characteristics, including its size, orientation, and location. The size of the image is determined by the object distance and the focal length of the lens. The orientation of the image is determined by whether the object is located in front of or behind the lens.
The location of the image is determined by the thin lens equation.
Applications
Thin lenses are used in a wide variety of applications, including cameras, telescopes, and microscopes. In cameras, thin lenses are used to focus light on the film or sensor. In telescopes, thin lenses are used to gather light from distant objects.
In microscopes, thin lenses are used to magnify small objects.
Answers to Common Questions: Thin Lenses. Object O Stands On The Central Axis
What is the significance of the central axis in thin lens optics?
The central axis of a thin lens is a crucial reference line that passes through the optical center of the lens and is perpendicular to both surfaces. It serves as the axis of symmetry for the lens and plays a key role in determining the behavior of light rays passing through the lens.
How does the position of an object on the central axis affect image formation?
The position of an object on the central axis relative to the thin lens determines the location and characteristics of the resulting image. Objects placed at different distances from the lens produce images at different distances and with varying magnifications.
What is the lens equation, and how is it used in thin lens optics?
The lens equation is a fundamental formula that relates the object distance (u), image distance (v), and focal length (f) of a thin lens. It is given by the equation 1/u + 1/v = 1/f. This equation allows us to calculate the image distance or object distance when the other two parameters are known.